Механизм генерации взрывоэмиссионных центров в вакуумном разряде при взаимодействии плотной плазмы катодного пятна с микронеоднородностями поверхности катода.

Одним из важных аспектов эктонной теории вакуумного разряда является вопрос о появлении новых (или вторичных) взрывоэмиссионных центров - эктонов, которые обеспечивали бы самоподдержание разряда. В этом направлении предложена и развита двумерная нестационарная модель инициирования новых взрывоэмиссионных центров при взаимодействии плазмы катодного пятна вакуумной дуги с микровыступами поверхности катода. В данной модели мы предполагаем, что над поверхностью катода находится плазма катодного пятна с концентрацией ионов на границе слоя пространственного заряда n_i и температурой электронов T_e. Форма поверхности микровыступа задается функцией Гаусса z_s=hexp(-(r/d)²), где h - высота, d - определяет радиус основания r_m, который определяется при z_s=0.1h . Геометрию микровыступа удобно характеризовать коэффициентом усиления плотности тока B_i=S/pi*r_m² , где S-площадь поверхности. В виду того, что толщина слоя пространственного заряда много меньше характерных размеров микровыступа, параметры слоя рассматриваются в одномерном (локальном) приближении. Расчет температурного поля в катоде проводится на основе уравнения теплопроводности. Омическое электрическое поле U и плотность тока в катоде определяется на основе уравнения непрерывности, что позволяет рассчитать Джоулев источник тепла. Для расчета плотности тока ионов, предполагаем, что ионы представляют собой моноэнергетические частицы, поступающие с границы слоя пространственного заряда с "бомовской" скоростью. При этом все ионы рекомбинируют на поверхности катода. Поток ионов из плазмы приносит на катод энергию, которая обуславливает соответствующий вклад в поверхностный источник тепла. Эмиссионные характеристики вычисляются численно в ВКБ приближении с учетом сдвига химпотенциала, обусловленного существенным повышением температуры катода. Для расчета электрического поля на поверхности катода используется обобщенное уравнение Маккоуна с учетом объемного заряда электронов, двигающихся из плазмы на катод.

Численное моделирование процесса разогрева микровыступа показало, что процесс поглощения энергии микровыступом, обусловленный потоком ионов из плазмы катодного пятна, и наличие электрического поля слоя пространственного заряда вблизи поверхности катода обеспечивают необходимую "затравочную" мощность потока тепла для развития процесса джоулева разогрева микровыступа и последующего микровзрыва при значениях плотности ионного тока на катод 10⁶~10⁷ А·см^-2 и коэффициенте усиления плотности тока микровыступом в несколько единиц.

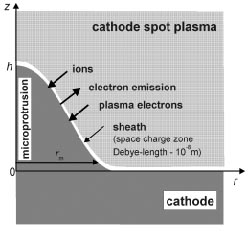
Рис. 1. Геометрия задачи и схематическое представление потоков заряженных частиц на границе раздела катод-плазма.

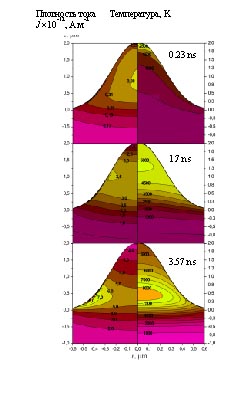
Рис.2. Пространственное распределение температуры (справа) и модуля плотности тока (слева) в различные моменты времени развития тепловой неустойчивости. Расчетные параметры: n_i =10²⁶ м^-3, T_e=2 эВ, ( j_i=5.6*10¹⁰ A/м² ), =4.:

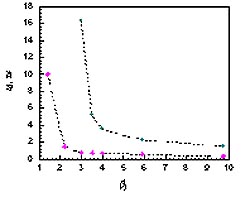
Рис. 3. Зависимость времени задержки до взрыва от (геометрии микровыступа):
green - n_i=10²⁶ m^-3 T_e=2 eV ( j_i=5.6*10¹⁰ A/m² ),
purple - n_i =1.8*10²⁶ m^-3 T_e=2 eV ( j_i=1.1*10¹¹ A/m² ).